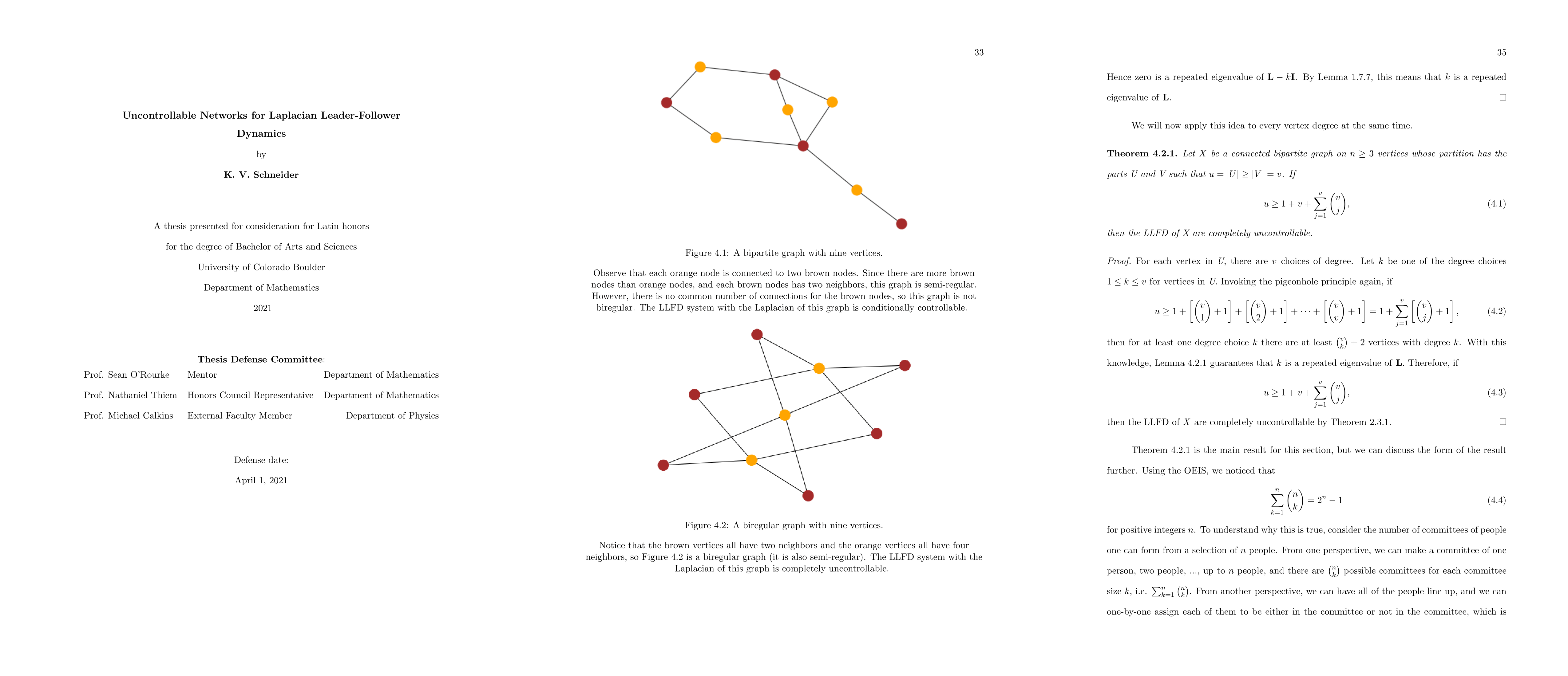
In this paper, we study characterizations of controllability for Laplacian leader-follower dynamics. Our discussion relies on the classification of graphs (networks) into three controllability classes: essentially controllable, completely uncontrollable, and conditionally controllable. In particular, this paper will show characteristics of graphs and their Laplacian matrices which give rise to complete uncontrollability. The controllability classes mentioned require the additional specification of the control vectors; here, we focus on the set of binary control vectors. We show that any Laplacian matrix with repeated eigenvalues will always have completely uncontrollable Laplacian leader-follower dynamics. This fact will allow us to make several deductions regarding the controllability properties of certain graph structures. Specifically, we prove that every circulant graph will have completely uncontrollable Laplacian leader-follower dynamics. We also show that for any biregular graph, if the difference in size between the two vertex sets is greater than one, then the Laplacian leader-follower dynamics are completely uncontrollable. In addition, we prove a similar bound for bipartite graphs in general.